개요
어떤 문제들은 입력을 짧게 치환해도 상관없는 경우가 있습니다. 이 문제가 그러한 것 중의 하나이며, 이 문제를 쉽게 풀려면 연속된 구간을 압축해야 합니다. 특정 값이 연속되는 구간은 나중에 같이 뒤집혀져야 하므로, 각 구간을 대표값 하나로 축약할 수 있겠죠.
축약 전:
1100000011축약 후:
101직관적으로 풀기
입력형식 되새김하기
이제 우리는 숫자가 연속되는 경우를 생각할 필요가 없습니다. from을 to로 바꿔야 한다고 했을 때, 다음과 같이 간략화된 입력만 생각하면 되는 것입니다.
from으로 시작하는 경우:
from
from-to
from-to-from
from-to-from-to
...
...to로 시작하는 경우:
to
to-from
to-from-to
to-from-to-from
...결과의 최대값 유추하기
이 문제를 푸는, 가장 간단하게 떠올릴 수 있는 방법은 모든 from을 to로 뒤집는 것이겠죠? 따라서 최소횟수는 적어도 from의 개수를 넘지 않는다는 것을 이끌어낼 수 있습니다.

from을 to로 바꾸는 최소횟수:
0 -> 1: 최대 0의 개수를 넘지 않는다.1 -> 0: 최대 1의 개수를 넘지 않는다.
다르게 뒤집을 수 있나?
새로운 방법 찾기
각각의 from을 to로 바꾸는 것 말고, 다른 방식으로 뒤집을 수 있는 방법이 있을까요? 그러한 방법이 있다면 from으로 둘러쌓인 연속된 구간이 동시에 뒤집어지는 형태겠죠.
증명해보자면, 먼저 각각의 from을 to로 바꾸는 방식은 1개 구간만 뒤집는 방법이므로, 이 방법이 최적이 아니라면 2개 이상의 연속된 구간을 동시에 뒤집는 방법이겠죠.
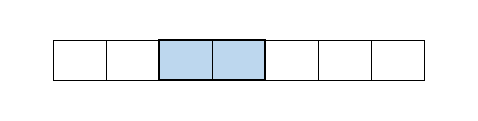
이렇게 만들어진 연속된 구간에서, 양쪽 둘 중 하나가 to인 경우에는 to를 빼버려서 구간을 축소하는 것이 더 효율적인 선택입니다. 굳이 영역에 포함시켜서 from으로 만들 이유가 있냐는 것이죠. 중간에 끼어있는 to는 어쩔 수 없이 포함된 것이지만, 양쪽끝의 to는 빠질려면 빠질 수 있거든요.

또한 입력에서 from과 to는 교대로 나타나므로, 양쪽 둘이 to가 아니게 만드려면 구간의 길이는 홀수여야 함을 알 수 있습니다.
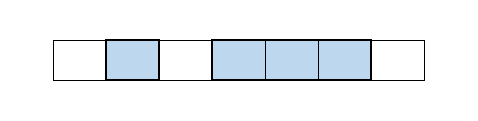
이 방법으로도 풀어보기
기존의 방식(1개씩 뒤집기)과 새로운 방식(N개 동시에 뒤집기) 둘 중에 어느 것이 더 뛰어난지 명확하게 판단할 수 없으므로, 두 방식으로 모두 풀어봐야겠죠. 따라서 새로운 방식으로 문제를 어떻게 풀 수 있는지 생각해야 합니다.
먼저 위에서 추론한 내용을 바탕으로, 새로운 방식이 적용되는 부분구간의 형태는 다음과 같습니다:
- 구간의 길이는 홀수
from으로 둘러쌓여야 함
from
from-to-from
from-to-from-to-from
from-to-from-to-from-to-from위의 부분구간은 동시에 뒤집히기 때문에, 다음과 같이 변환되고:
to
to-from-to
to-from-to-from-to
to-from-to-from-to-from-to양쪽의 to는 필요없으므로, 다시 다음과 같이 축소됩니다 :
x
from
from-to-from
from-to-from-to-from재귀적으로 풀어갈 수 있다는 것을 눈치채셨나요? 이 방법으로 구간의 길이가 2N+1인 부분구간을 뒤집을 때 필요한 횟수는 N+1이고 이것은 from의 개수입니다.
즉 각각을 뒤집으나 동시에 뒤집으나 차이가 없다는 것을 알아냈으므로, 원래 입력을 무수히 많은 부분구간으로 분할해도 from의 개수에서 벗어나지 않을겁니다. 부분구간을 풀어내도 from의 개수가 튀어나오기 때문입니다.
2 2
(from-to-from)-to-(from-to-from)따라서, 둘 중 하나가 정답입니다.
from=0, to=1인 경우, 양쪽 끝이 아닌0의 개수.from=1, to=0인 경우, 양쪽 끝이 아닌1의 개수.
추가 테스트케이스
1번
input :
0expect:
02번
input :
0011100expect:
13번
input :
11000001expect:
14번
input :
1010expect:
25번
input :
101010101expect:
4'# Foundation > 백준풀이' 카테고리의 다른 글
| 백준 2437 풀이 및 해설 (13) | 2020.12.02 |
|---|---|
| 백준 2136 풀이 및 해설 (1) | 2020.11.28 |
| [LCS] 백준 1958 :: LCS 3 (0) | 2019.07.10 |
| [LCS] 백준 9252 :: LCS 2 (0) | 2019.07.10 |
| [LCS] 백준 9251 :: LCS (0) | 2019.07.10 |



