개요
매우 복잡해보이는 문제가 그림으로 풀면 매우 단순하게 풀리는 경우는 그리 드문일이 아닙니다. 이 문제는 수학적 귀납법으로도 풀 수 있지만, 수직선을 사용하면 훨씬 직관적이고 쉽게 풀립니다. 핵심은 측정할 수 있는 무게의 구간을 끊기지 않게 확장시키는 것 입니다.
핵심
현재 닫힌구간 [1, 10]을 측정할 수 있는 상태에서 무게가 5인 무게추가 더 주어졌다면, 기존에 측정할 수 있었던 무게 + 5를 측정할 수 있으므로, 1부터 10까지 순회하면서 5를 더한값을 추가로 측정할 수 있습니다. 즉, 닫힌구간 [1+5, 10+5]를 추가로 측정할 수 있습니다.

그렇다면 닫힌구간 [1, 5]를 측정할 수 있는 상태에서 무게가 7인 무게추가 더 주어지면 어떻게 될까요? 닫힌구간 [1, 12]를 전부 커버할 수 있을까요? 아래 그림을 살펴보면 닫힌구간 [6, 7]이 측정될 수 없음을 알 수 있습니다.

예제 풀이
예제입력 1번에 해당 아이디어를 적용해보겠습니다.
7
3 1 6 2 7 30 1측정할 수 없는 가장 가벼운 무게를 구하는데, 무거운 추부터 사용하는 것은 올바르지 않으므로, 다음과 같이 오름차순으로 정렬합니다.
7
1 1 2 3 6 7 30Step 1
v
1 1 2 3 6 7 30처음에는 측정할 수 있는 구간이 없으므로 [0, 0]으로 가정합니다. 이 상태에서 무게가 1인 무게추가 더 주어지면 [1, 1]을 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 1]로 퉁칠 수 있습니다.

Step 2
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 1]인 상태에서 무게가 1인 무게추가 더 주어지면 [1, 2]를 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 2]로 퉁칠 수 있습니다.
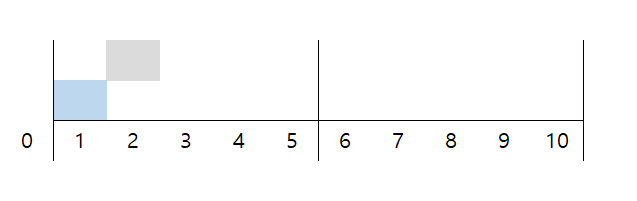
Step 3
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 2]인 상태에서 무게가 2인 무게추가 더 주어지면 [2, 4]를 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 4]로 퉁칠 수 있습니다.
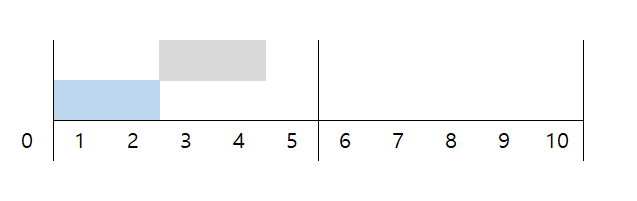
Step 4
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 4]인 상태에서 무게가 3인 무게추가 더 주어지면 [3, 7]를 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 7]로 퉁칠 수 있습니다.

Step 4
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 7]인 상태에서 무게가 6인 무게추가 더 주어지면 [6, 13]을 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 13]으로 퉁칠 수 있습니다.

Step 5
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 13]인 상태에서 무게가 7인 무게추가 더 주어지면 [7, 20]을 추가로 측정할 수 있습니다. 두 구간은 끊어지지 않으므로 [0, 20]으로 퉁칠 수 있습니다.

Step 6
v
1 1 2 3 6 7 30측정가능한 구간이 [0, 20]인 상태에서 무게가 30인 무게추가 더 주어지면 [30, 50]을 추가로 측정할 수 있습니다. 두 구간은 연속되지 않으므로, 이 두 구간 중간에 위치한 구간은 측정할 수 없습니다. 따라서 측정 불가능한 최소 무게는 21입니다.

누적합으로 풀기
예제풀이로 알 수 있듯이, 이 문제의 키 포인트는 이전구간과 새롭게 생긴 구간이 연속되는가?를 판단하는 것입니다.
지금까지 구간이 끊기지 않았다면, 기존 구간은 [0, E]의 형태일 것이고, E는 지금까지 사용했던 무게추의 누적합과 같을 것입니다. 이유를 좀 더 설명해보자면 E는 측정할 수 있는 무게의 최대값이죠? N개의 무게추를 사용하여 측정할 수 있는 무게의 최대치는, N개 모두를 사용했을 때의 무게이기 때문입니다.
거의 다왔습니다. [0, acc[i-1]]인 상태에서 무게가 weights[i]인 무게추가 더 주어진다면, 구간 정보는 다음과 같고:
- 기존 구간 :
[0, acc[i-1]] - 신규 구간 :
[weights[i], acc[i]]
위의 두 구간이 끊어지지 않으려면 weights[i] <= acc[i-1] + 1을 만족해야 함을 알 수 있습니다.
예제입력에서는 i=7에서 조건이 만족되지 않으므로, 7번째 무게추가 들어올 때 구간이 끊어졌겠죠? 끊어진 구간의 첫 번째 값이 측정할 수 없는 최소값이므로, 21(=20+1)이 정답입니다.

추가 테스트케이스
1번
input :
1
1expect:
22번
input :
1
2 3expect:
13번
input :
4
1 1 1 1expect:
54번
input :
3
1 2 4 16expect:
85번
input :
7
3 1 6 2 7 30 1expect:
21'# Foundation > 백준풀이' 카테고리의 다른 글
| 백준 1439 풀이 및 해설 (1) | 2020.12.03 |
|---|---|
| 백준 2136 풀이 및 해설 (1) | 2020.11.28 |
| [LCS] 백준 1958 :: LCS 3 (0) | 2019.07.10 |
| [LCS] 백준 9252 :: LCS 2 (0) | 2019.07.10 |
| [LCS] 백준 9251 :: LCS (0) | 2019.07.10 |



